This is the page where you can access the answers to the four incredibly challenging "Puzzles for the Super Intelligent" that are in Dr. Fun's latest book entitled The Cleverest Puzzles on the Planet. The book will be published at an undisclosed date in 2013.
For the answer to the puzzle entitled A Perplexing Placement Problem:
This hint should get you started.
Did you try really hard to solve this puzzle or are you just curious about the answer?
If you haven�t given it your best shot, let me give you a hint. Then give it another try.

Hint: Stategically place the nine dots in a 5 x 5 matrix.

If you�re still stymied, this hint should give you a big boost.

Hint 2: Here�s half of the answer. Now place the other four dots.
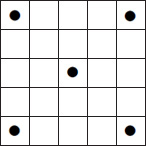
Okay. If you must, check out the answer.

Answer:
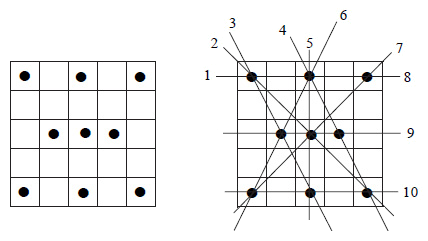
For the answer to the puzzle entitled The Timinator:
This hint should get you started.
Did you try really hard to solve this puzzle or are you just curious about the answer?
If you haven�t given it your best shot, let me give you a hint. Then give it another try.

Hint: Begin analyzing C-across, H-across, then G-down.
If you�re still stymied, this hint should give you a big boost.


Hint 2: The hardest part of this puzzle is getting started.
Here�s is how to begin. Note that all answers must be whole numbers.
- From C-across, Tim can�t be more that 8 years old.
- From H-across and due to the year of the puzzle being 2000, the first two digits must be 19.
Okay. If you must, check out the answer.


Answer: Here�s the sequence to arrive at the answer: Note that all answers must be whole numbers.
- From C-across, Tim can�t be more that 8 years old.
- From H-across and due to the year of the puzzle being 2000, the first two digits must be 19
- From G-down, Tim�s birth weight must be 8 lbs (the only common birth weight divisible by 4) so G-down must be 16.
- E-down must therefore be 107.
- Since G-down, Tim�s age in 8 full years is 16, then C-across must be 24.
- Since H-across is 1967, C-down must be 281.
- D-across must then be 888.
- A-across must therefore be 5328
- Lastly, B-down must be 25.
For the answer to the puzzle entitled A Weighty Problem:
This hint should get you started.
Did you try really hard to solve this puzzle or are you just curious about the answer?
If you haven�t given it your best shot, let me give you a hint. Then give it another try.

Hint: For the first weighing place four coins on each side of the scale. Then label those eight coins with the information gained from the weighing.
If you�re still stymied, this hint should give you a big boost.

Hint 2: Label the coins in accordance with the following.
G: coins established as genuine
H: coins suspected as being heavier than genuine
L: coins suspected as being lighter than genuine
X: coins not established as any of the above
Okay. If you must, check out the answer.

Answer: Label the coins in accordance with the follolwing legend.
G: coins established as genuine
H: coins suspected as being heavier than genuine
L: coins suspected as being lighter than genuine
X: coins not established as any of the above
*Subscripts refer to the coin number
Weighing #1:
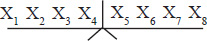
Possibilities:
(A) Balance: All eight coins are genuine. The next weighting is 2A.
(B) Unbalance: One of the 8 coins is counterfeit. All four remaining coins are genuine. Assume the left side of the scale goes down and right side goes up. Then the four coins on the left side are suspected as being heavy and are denoted by H1 H2 H3 H4 and the four coins on the right are denoted as L5 L6 L7 L8 . The next weighing is 2B.
Weighing #2A:

Possibilities:
(A) Balance: All coins are genuine. Weighing #3AA: The remaining coin X12 is the counterfeit coin. Simply weigh it against a genuine coin to determine if it is heavier or lighter than genuine.
(B) Unbalance: Assume the left side goes down. Then either X9 or X10 is heavy or X11 is light. Weighing #3AB: Weigh X9 against X10. If they balance, X11 is the counterfeit coin and it is lighter than genuine. If they do not balance, then the coin on the side that goes down has the counterfeit coin and it is heavier than genuine. Use similar reasoning if the right side of the scale goes down.
Weighing #2B:

Possibilities:
(A) Balance: all six coins are genuine. Therefore, either H3 or H4 must be the counterfeit coin. Weighing #3BA: Weigh H3 against H4. The side of the scale that goes down contains the counterfeit coin and it is heavier that genuine.
(B) Unbalance: Assume the left side goes down. Then either H1 is heavy or L7 or L8 is light. Weighing #3BB: Weigh L7 against L8. If they balance, H1 is the counterfeit coin and it is heavier than genuine. If it doesn�t balance, the side that goes up contain the counterfeit coin and it is lighter than genuine. Use similar reasoning if the right side of the scale goes down.
For the answer to the puzzle entitled An Ageless Conundrumm:
This hint should get you started.
Did you try really hard to solve this puzzle or are you just curious about the answer?
If you haven�t given it your best shot, let me give you a hint. Then give it another try.

Hint: Start by finding all the products of three numbers totaling 2450.
There are only ten combinations.
If you�re still stymied, this hint should give you a big boost.

Hint 2: Here�s how to determine the sets of three ages that multiply to 2450.
Because 2450 ends in the digit 0, one of the products must be a multiple of 5.
2450 divided by 5 = 490. Two ages that multiply to 490: 49 x 10 and 7 x 70 and 35 x 14
2450 divided by 10 = 245. Two ages that multiply to 245: 5 x 49 and 7 x 35
2450 divided by 25 = 98. Two ages that multiply to 98: 7 x 14 and 2 x 49
2450 divided by 35 = 70. Two ages that multiply to 70: 7 x 10 and 35 x 2
2450 divided by 50 = 49. Two ages that multiply to 49: 7 x 7
2450 divided by 70 = 35. Two ages that multiply to 35: 5 x 7
Okay. If you must, check out the answer.

Answer:
- First, determine all the products of three numbers that total 2450. Because 2450 ends in the digit 0, one of the products must be a multiple of 5. Also, remember since all numbers refer to ages, they must all be whole numbers.
- Determination of the products:
- 2450 divided by 5 = 490. Two ages that multiply to 490: 49 x 10 and 7 x 70 and 35 x 14
- 2450 divided by 10 = 245. Two ages that multiply to 245: 5 x 49 and 7 x 35
- 2450 divided by 25 = 98. Two ages that multiply to 98: 7 x 14 and 2 x 49
- 2450 divided by 35 = 70. Two ages that multiply to 70: 7 x 10 and 35 x 2
- 2450 divided by 50 = 49. Two ages that multiply to 49: 7 x 7
- 2450 divided by 70 = 35. Two ages that multiply to 35: 5 x 7
- Determination of the sum of each set of three ages.
- 5 + 49 + 10 = 64
- 5 + 7 + 70 = 145
- 5 + 35 + 14 = 54
- 10 + 5 + 49 = 64
- 10 + 7 + 35 = 42
- 25 + 7 + 14 = 46
- 25 + 2 + 49 = 76
- 35 + 7 + 10 = 52
- 35 + 35 + 2 = 72
- 50 + 7 + 7 = 64
- 70 + 5 + 7 = 82
- There are only two unique sets of three ages (in bold type) that have the same total. (Note that two of the three sets have the identical three ages). Now note that all other totals are different from each other. The organist obviously knows his own age. His age must be 64 because if his age had been any of the other totals, he would have had enough information to determine the three ages. Since two different sets totaled his age, he was not able to solve the puzzle. That�s why he needed more information.
- The organist was told that he would have enough information to determine the three ages after being told that the minister was older than the other three people. Now examine the two sets of ages: 10, 5, 49 and 50, 7, 7. If the minister was older that 50, the organist still would not know which of the two sets of ages is correct. The determination is only possible when the age of the minister is 50 (the highest age in one of the sets). Therefore the minister is 50 years old and the ages of the other three people are 10, 5 and 49. Case solved!